BLUEFISH - ENERGY HARVESTING DEVELOPMENT PROGRAMME

Weight analysis - Autonomous solar powered SWASH robot development for clean speed on water

DEVELOPMENT MODEL WEIGHT ANALYSIS - EUREKA

The same procedure is used to determine the mass of a vessel whether it is a model or a full size ship. The following is a rough guide or starting point from which the actual hull parts and components will be weighed in as they are sourced, etc. Obviously, the design of the vessel ultimately determines the displacement and we must be sure that the development model accurately reflects that of the full size ship - or we will be wasting our time conducting testing and experimentation. 

It is likely that we will need to ballast the model to simulate actual load conditions in the full size ship. We should also consider that our tests will mostly be conducted in fresh water which is 1 kg/liter as opposed to 1.025 kg/liter for seawater - meaning that the full size vessel will have that advantage also, unless that is the operators intend navigating the Amazon.

So far we are well within our target. Let's hope it stays that way as the last few gadgets are fitted. The weight of a ship always goes up during fitting out, never down.

FULL SIZE SHIP TARGET WEIGHTS

IMPROVING THE POWER TO WEIGHT RATIO

The mass of a vessel ultimately determines the resistance to movement through the water. For the purpose of discussion we are taking it that the ship the object of our focus, is as form-efficient (slippery) as is possible.

There are many ways to reduce weight. We can use exotic materials such as aramid and graphite fibers, or we can design an aluminium structure to use less material, for which a bridge across a river is a good starting point when analyzing loads and sections. Ship design has changed little for centuries, simply because there has been no need to alter the basic concept of a log floating in the water with tapered ends. 

Structurally, that is like comparing a worm with a flying insect, but there has been no reason to consider lighter, intricate structures, except perhaps in racing catamarans. Many insects have mastered land, air and water travel by design; a minor miracle. Like an insect, we are looking for very lightweight wings to support our solar panels. It does not stop there with the wings; we must include the frame that supports the wings - and that frame must in turn attach to our submerged hull.

DISPLACEMENT

In fluid mechanics, occurs when an object is immersed in a fluid, pushing it out of the way and taking its place. The volume of the fluid displaced can then be measured, and from this the volume of the immersed object can be deduced (the volume of the immersed object will be exactly equal to the volume of the displaced fluid).

An object that sinks displaces an amount of fluid equal to the object's volume. Thus buoyancy is expressed through Archimedes' principle, which states that the weight of the object is reduced by its volume multiplied by the density of the fluid. If the weight of the object is less than this displaced quantity, the object floats; if more, it sinks. The amount of fluid displaced is directly related (via Archimedes' Principle) to its weight.

In the case of an object that sinks (is totally submerged), the volume of the object is displaced. In the case of an object that floats, the amount of fluid displaced will be equal in weight to the displacing object.

APPLICATIONS

This method can be used to measure the volume of a solid object, even if its form is not regular. Several methods of such measuring exist. In one case the increase of water level is registered as the object is immersed into the water. In the second case the object is immersed into a vessel full of water, causing it to overflow. Then the spilled water is collected and its volume measured. In the third case the object is suspended under the surface of the water and the increase of weight of the vessel is measured. It is equivalent to the weight of the amount of water that has the volume equal to the one of the suspended object.

The weight of an object or substance can be measured by floating a sufficiently buoyant receptacle in the cylinder and noting the water level. After placing the object or substance in the receptacle, the difference in weight of the water level volumes will equal the mass of the object.

SHIP DISPLACEMENT

A ship's displacement or displacement tonnage is the weight of the water that a ship displaces when it is floating; the term is defined ordinarily such that the ship's fuel tanks are full and all stores are aboard. The term is applied usually to naval vessels. Displacement is the actual weight of the ship, since a floating body displaces its own weight in water (Archimedes' principle). Another way of thinking about displacement is the weight of the water that would spill out of a completely filled container were the ship placed into it.

A number of synonymous terms exist for this maximum weight, such as loaded displacement, full load displacement and designated displacement. As a measurement of weight, displacement should not be confused with similarly named measurements of volume or capacity such as net tonnage, gross tonnage, or deadweight tonnage.

The density (weight per unit of volume) of water can vary. For example, the average density of seawater at the surface of the ocean is 1025 kg/m³ (10.25 lb/ga, 8.55 lb/US gallon); fresh water on the other hand has a density of about 1000 kg/m³ (10.00 lb/ga, 8.35 lb/US gallon). Consider a 100-ton ship passing from a saltwater sea into a freshwater river. It always displaces exactly 100 tons of water, but it has to displace a greater volume of fresh water to amount to 100 tons. Therefore it would sit slightly lower in the water in the freshwater river than it would in the saltwater sea.

It can be useful to know a ship's displacement when it is unloaded or loaded partially. Terms for these measurements include light displacement, standard displacement, and normal displacement. These terms are defined below.

CALCULATION

The traditional method for determining a ship's actual displacement is by use of draft marks. A merchant vessel has six sets of draft marks: forward, midships, and astern on both the port and starboard sides. These drafts can allow the determination of a ship's displacement to an accuracy of 0.5%. First, the individual drafts are averaged to find a mean draft. Then the mean draft is entered into the ship's hydrostatic tables, giving a displacement.

Computers have been used to assist hydrostatic calculations, such as determining displacement, since the 1950s. The first were mechanical computers, similar to slide rules which could convert cargo levels to values such as deadweight tonnage, draft, and trim. Since the introduction of electronic digital computers, computer programs have been developed to meet these needs.

MARINE TERMS

A number of measurements of displacement are defined when the ship is in a special state, such as when it is completely full or completely empty. These special types of displacement are discussed below.
Full or deep load or loaded displacement

Full load displacement and loaded displacement have almost identical definitions.

Full load displacement is defined as the displacement of a vessel when floating at its greatest allowable draft as established by classification societies. For warships, an arbitrary full load condition is established. Deep load condition means full ammunition and stores, with most available fuel capacity used.

Loaded displacement is defined as the weight of the ship including cargo, passengers, fuel, water, stores, dunnage and such other items necessary for use on a voyage, which brings the ship down to its load draft.

Standard displacement

The standard displacement, also known as Washington displacement, is a term defined by the Washington Naval Treaty of 1922. It is defined as the displacement of the ship complete, fully manned, engined, and equipped ready for sea, including all armament and ammunition, equipment, outfit, provisions and fresh water for crew, miscellaneous stores, and implements of every description that are intended to be carried in war, but without fuel or reserve boiler feed water on board. The omission of fuel and water was to avoid penalizing the British, who had great global commitments and required greater fuel loads, and especially the United States, which had global commitments almost as great but with fewer bases to provide fueling than the Royal Navy.

Light displacement

Light displacement (LDT) is defined as the weight of the ship excluding cargo, fuel, ballast, stores, passengers, crew, but with water in boilers to steaming level.

Normal displacement

This rare term has been used to mean the ship's displacement "with all outfit, and two-thirds supply of stores, ammunition, etc., on board."

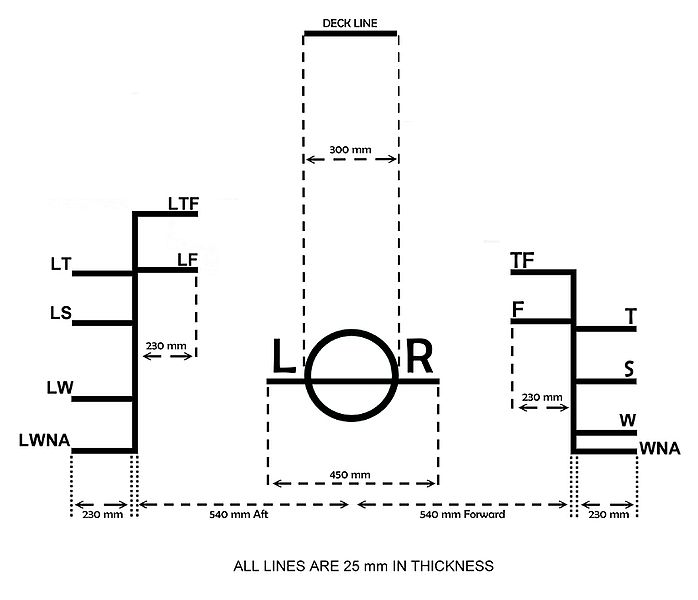
THE PLIMSOLL LINE

A Plimsoll Line is the line where the hull of a ship meets the surface of the water, in concept or reality. Specifically, it is also the name of a special marking, also known as the International Load Line or water line (positioned amidships), that indicates the draft of the ship and the legal limit to which a ship may be loaded for specific water types and temperatures in order to safely maintain buoyancy, particularly with regard to the hazard of waves that may arise. Temperature affects the level because warm water provides less buoyancy, being less dense than cold water, as does salinity because fresh water is less dense than salty seawater. For vessels with displacement hulls, the hull speed is determined by, amongst other things, the waterline length. In a sailing boat, the waterline length can change significantly as the boat heels, and can dynamically affect the speed of the boat.

The purpose of a load line is to ensure that a ship has sufficient freeboard (the height from the water line to the main deck) and thus sufficient reserve buoyancy, indisputable seen from the outside.

In aircraft design, the term "waterline" refers to the vertical location of items on the aircraft. This is the (normally) "Z" axis of an XYZ coordinate system, the other two axes being the Fuselage Station (X) and Buttock Line (Y).

INVENTOR: SAMUEL PLIMSOLL

The purpose of a load line is to ensure that a ship has sufficient freeboard (the height from the water line to the main deck) and thus sufficient reserve buoyancy. The freeboard of commercial vessels is measured between the lowest point of the uppermost continuous deck at side and the waterline and this must not be less than the freeboard marked on the Load Line Certificate issued to that ship. All commercial ships, other than in exceptional circumstances, have a load line symbol painted amidships on each side of the ship. This symbol must also be permanently marked, so that if the paint wears off it remains visible. The load line makes it easy for anyone to determine if a ship has been overloaded. The exact location of the Load Line is calculated and/or verified by a Classification Society and that society issues the relevant certificates. This marking was invented in the 1870s by Samuel Plimsoll.
History

The first official loading regulations are thought to date back to maritime legislation originating with the kingdom of Crete in 2,500 BC when vessels were required to pass loading and maintenance inspections. Roman sea regulations also contained similar regulations.

In the Middle Ages the Venetian Republic, the city of Genoa and the Hanseatic league required ships to show to a load line. In the case of Venice this was a cross marked on the side of the ship, and of Genoa three horizontal lines.

The first 19th century loading recommendations were introduced by Lloyd's Register of British and Foreign Shipping in 1835, following discussions between shipowners, shippers and underwriters. Lloyds recommended freeboards as a function of the depth of the hold (three inches per foot of depth). These recommendations, used extensively until 1880, became known as "Lloyd's Rule".

In the 1860s, after increased loss of ships due to overloading, a British MP, Samuel Plimsoll, took up the load line cause. A Royal Commission on unseaworthy ships was established in 1872, and in 1876 the United Kingdom Merchant Shipping Act made the load line mark compulsory, although the positioning of the mark was not fixed by law until 1894. In 1906, laws were passed requiring foreign ships visiting British ports to be marked with a load line. It was not until 1930 (The 1930 Load Line Convention) that there was international agreement for universal application of load line regulations.

In 1966 a Load Lines Convention was held in London which re-examined and amended the 1930 rules. The 1966 Convention has since seen amendments in 1971, 1975, 1979, 1983, 1995 and 2003.

LOAD LINE MARKS

The original "Plimsoll Mark" was a circle with a horizontal line through it to show the maximum draft of a ship. Additional marks have been added over the years, allowing for different water densities and expected sea conditions.

Letters may also appear to the sides of the mark indicating the classification society that has surveyed the vessel's load line. The initials used include AB for the American Bureau of Shipping, LR for Lloyd's Register, GL for Germanischer Lloyd, BV for Bureau Veritas, IR for the Indian Register of Shipping, RI for the Registro Italiano Navale, NK for Nippon Kaiji Kyokai, and NV for Det Norske Veritas. These letters should be approximately 115 millimetres in height and 75 millimetres in width. The Load Line Length is referred to during and following load line calculations.

The letters on the load line marks have the following meanings:

TF – Tropical Fresh Water
F – Fresh Water
T – Tropical Seawater
S – Summer Temperate Seawater
W – Winter Temperate Seawater
WNA – Winter North Atlantic

ARCHIMEDES

Archimedes' principle indicates that the upward buoyant force exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. Archimedes of Syracuse formulated this principle, which bears his name.

EXPLANATION

In his treatise on hydrostatics, On Floating Bodies, Archimedes states:

"Any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object."

— Archimedes of Syracuse


We may observe for any immersed object that the volume of the submerged portion equals the volume of fluid it displaces. E.g., by submerging in water half of a sealed 1-litre container, we displace a half-litre volume of fluid, regardless of the container's contents. If we fully submerge the same container, we then displace one litre of fluid.

Also, we may observe for any immersed object that buoyancy = weight of displaced fluid. E.g., if by submerging a container in water we displace a 1-kilogram mass of fluid, then the buoyant force of the water equals the weight—about 9.8 Newtons in this example—of the displaced mass. With respect to objects of constant volume, displacement remains constant regardless of an object's depth of submersion or its composition.

Objects weigh more in air than they do in water. If a 30-kilogram object displaces 20 kilograms of fluid when immersed, then its apparent weight equals the weight of 10 kilograms (98 newtons). This is because the 30 kilograms of weight pushing down are counteracted by the 20 kilograms of weight pushing up. Similarly, when submerged, a 3-kilogram block may have an apparent weight of 1 kilogram. The "missing weight" is equal to the weight of the water displaced, the weight of 2 kilograms (19.6 newtons), which is the buoyant force. The apparent weight of a submerged object is its weight under standard conditions minus the buoyant force.

Because the density of water is 1 g/cm3 (or 1 kg/L), an object that has displaced 20 kg of water, must have a volume of 20 litres. Archimedes’ Principle can therefore be used to measure the volume of any solid, regardless of its shape. If the 30 kg object appears to weigh an equivalent of 10 kg when immersed in water, it must have displaced 20 kg of water, or in other words 20L of water.

So,

Volume of Object (in Litres) = Weight of Object in Air (in kilograms) – Weight of Object in Water (in kilograms)

or

Volume of Object (in millilitres or cubic centimetres) = Weight of Object in Air (in grams) – Weight of Object in Water (in grams)

(This equation assumes that the object is completely submerged, and has a density of at least 1 kg/L)

Consider a completely submerged cube. The fluid exerts pressure on all six faces, but as long as the cube is not tilted, the forces on the four vertical faces balance each other out. The pressure difference between the bottom and the top face is directly proportional to the height (difference in depth). Multiplying the pressure difference with the area of a face gives the net force on the cube - the buoyancy, or the weight of the fluid displaced. It makes no difference how deep the cube is placed because, although the pressures are greater with increasing depths, the difference between the pressure up against the bottom of the cube and the pressure down against the top of the cube is the same at any depth. Whatever the shape of the submerged body, the buoyant force is equal to the weight of the fluid displaced.


PRINCIPLE OF FLOTATION

Archimedes' principle relates buoyant force and displacement of fluid. However, the concept of Archimedes' principle can be applied when considering why objects float. Proposition 5 of Archimedes' treatise On Floating Bodies states that:

"Any floating object displaces its own weight of fluid."

                                                                                     — Archimedes of Syracuse

In other words, for a floating object on a liquid, the weight of the displaced liquid is the weight of the object. Thus, only in the special case of floating does the buoyant force acting on an object equal the objects weight. Consider a 1-ton block of solid iron. As iron is nearly eight times denser than water, it displaces only 1/8 ton of water when submerged, which is not enough to keep it afloat. Suppose the same iron block is reshaped into a bowl. It still weighs 1 ton, but when it is put in water, it displaces a greater volume of water than when it was a block. The deeper the iron bowl is immersed, the more water it displaces, and the greater the buoyant force acting on it. When the buoyant force equals 1 ton, it will sink no farther.

When any boat displaces a weight of water equal to its own weight, it floats. This is often called the "principle of flotation": A floating object displaces a weight of fluid equal to its own weight. Every ship, submarine, and dirigible must be designed to displace a weight of fluid equal to its own weight. A 10,000-ton ship must be built wide enough to displace 10,000 tons of water before it sinks too deep in the water. The same is true for vessels in air (as air is a fluid): a dirigible that weighs 100 tons displaces at least 100 tons of air. If it displaces more, it rises; if it displaces less, it falls. If the dirigible displaces exactly its weight, it hovers at a constant altitude.

It is important to realize that, while they are related to it, the principle of flotation and the concept that a submerged object displaces a volume of fluid equal to its own volume are not Archimedes' principle. Archimedes' principle, as stated above, equates the buoyant force to the weight of the fluid displaced.

ARCHIMEDES PRINCIPLE

The most widely known anecdote about Archimedes tells of how he invented a method for determining the volume of an object with an irregular shape. According to Vitruvius, a votive crown for a temple had been made for King Hiero II, who had supplied the pure gold to be used, and Archimedes was asked to determine whether some silver had been substituted by the dishonest goldsmith. Archimedes had to solve the problem without damaging the crown, so he could not melt it down into a regularly shaped body in order to calculate its density. While taking a bath, he noticed that the level of the water in the tub rose as he got in, and realized that this effect could be used to determine the volume of the crown. For practical purposes water is incompressible, so the submerged crown would displace an amount of water equal to its own volume. By dividing the mass of the crown by the volume of water displaced, the density of the crown could be obtained. This density would be lower than that of gold if cheaper and less dense metals had been added. Archimedes then took to the streets naked, so excited by his discovery that he had forgotten to dress, crying "Eureka!" (Greek: "εὕρηκα!," meaning "I have found it!"). The test was conducted successfully, proving that silver had indeed been mixed in.

The story of the golden crown does not appear in the known works of Archimedes. Moreover, the practicality of the method it describes has been called into question, due to the extreme accuracy with which one would have to measure the water displacement. Archimedes may have instead sought a solution that applied the principle known in hydrostatics as Archimedes' principle, which he describes in his treatise On Floating Bodies. This principle states that a body immersed in a fluid experiences a buoyant force equal to the weight of the fluid it displaces. Using this principle, it would have been possible to compare the density of the golden crown to that of solid gold by balancing the crown on a scale with a gold reference sample, then immersing the apparatus in water. The difference in density between the two samples would cause the scale to tip accordingly. Galileo considered it "probable that this method is the same that Archimedes followed, since, besides being very accurate, it is based on demonstrations found by Archimedes himself." In a 12th-century text titled Mappae clavicula there are instructions on how to perform the weighings in the water in order to calculate the percentage of silver used, and thus solve the problem. 

The Latin poem Carmen de ponderibus et mensuris of the 4th or 5th century describes the use of a hydrostatic balance to solve the problem of the crown, and attributes the method to Archimedes.

LINKS & REFERENCE

http://en.wikipedia.org/wiki/Waterline

http://en.wikipedia.org/wiki/Archimedes%27_principle

http://www.solarnavigator.net/inventors/archimedes.htm

http://en.wikipedia.org/wiki/Archimedes%27_principle

http://en.wikipedia.org/wiki/Displacement_%28fluid%29

http://en.wikipedia.org/wiki/Displacement_%28ship%29

http://www.cyberiad.net/leo.htm

The models seen on these pages are being constructed under license for testing of the robotic, solar and wind energy harvesting systems, - using radio control initially, switching to computer micro-controller for fully autonomous robotic control.

This page is Copyright © 2014 Bluebird Marine Systems Ltd. The names Bluebird™, Bluefish™, SeaNet™, and the blue bird & fish in flight logos are trademarks. All other trademarks are hereby acknowledged.